Synthèses des programmes - Sciences
Retrouvez les synthèses des nouveaux programmes en Mathématiques • Physique-Chimie • SVT • Enseignement Scientifique.
MATHÉMATIQUES :
> TÉLÉCHARGEZ LA 2de > TÉLÉCHARGEZ LA 1RE > TÉLÉCHARGEZ LA TLE
PHYSIQUE-CHIMIE :
> TÉLÉCHARGEZ LA 2de > TÉLÉCHARGEZ LA 1RE > TÉLÉCHARGEZ LA TLE
SVT :
> TÉLÉCHARGEZ LA 2de > TÉLÉCHARGEZ LA 1re
ENSEIGNEMENT SCIENTIFIQUE :
> TÉLÉCHARGEZ LA 1RE > TÉLÉCHARGEZ LA TLE
MathÉMATIQUEs 2de • 1re • TLE
• Les mathématiques font partie du tronc commun de la classe de 2de, à raison de 4 h par semaine.
• Dans la voie générale, à partir de la Première, les mathématiques ne font pas partie du tronc commun, et deviennent un enseignement de spécialité à raison de 4 h par semaine en Première et 6 h par semaine en Terminale pour l’enseignement de spécialité.
LE PROGRAMME DE LA SECONDE À LA TERMINALE
PRINCIPES GÉNÉRAUX
OBJECTIFS
Le préambule du programme donne les objectifs de l’enseignement des mathématiques, notamment :
• La consolidation des acquis de l’année précédente, en 2de l’acquisition d’une culture mathématique et en 1re la maîtrise de l’abstraction.
• La préparation du choix de l’orientation : choix de la spécialité pour la voie générale et choix de la série pour la voie technologique et en 1re éventuellement l’enseignement optionnel de mathématiques expertes, ou choix de l’enseignement optionnel de mathématiques complémentaires)
• L’importance de la diversité de l’activité de l’élève (résolutions de problèmes, questions flash, activités rituelles, travail collectif, oral, etc.), aussi bien en classe que lors du travail personnel hors du temps scolaire
• L’utilisation de logiciels, notamment pour visualiser, représenter, calculer, simuler, mais aussi programmer (en utilisant le langage Python)
• La place de l’oral (argumenter, préciser sa pensée, expliciter son raisonnement) et l’importance des traces écrites. Importance particulière pour les élèves qui choisiront les mathématiques comme enseignement de spécialité en terminale et qui passeront l’épreuve orale du Baccalauréat en lien avec cet enseignement)
• L'importance de l'écrit (trace de cours claire, explicite et structurée)
• Le travail de la démonstration (une liste de démonstrations exemplaires figure dans chaque sous-partie du programme) (► liste de toutes les démonstrations au programme dans le pdf à télécharger)
UNE NOUVELLE PRÉSENTATION DES PROGRAMMES
• Chaque partie du programme contient en introduction :
- Les objectifs de la partie
- Les éléments d’histoire des mathématiques qui pourront éclairer les notions étudiées dans la partie
• Chaque sous-partie du programme contient généralement, en plus des contenus et capacités attendues habituellement présents dans les programmes de mathématiques :
- Une rubrique « Démonstrations » listant les démonstrations exemplaires que l’élève doit étudier, soit présentées par l’enseignant, soit élaborées par l’élève (> liste de toutes les démonstrations au programme dans le PDF à télécharger)
- Une rubrique « Exemples d’algorithme » listant les algorithmes qui peuvent être étudiés en lien avec les contenus et capacités de la sous-partie
- Une rubrique « Approfondissements possibles » (qui ne sont pas obligatoires), permettant une différenciation pédagogique.
le programme de 2de
VISION SYNOPTIQUE DU PROGRAMME
• Nombres et calculs
Manipuler les nombres réels dont ensembles de nombres, intervalles, distance entre deux nombres
Utiliser les notions de multiple, diviseur et de nombre premier
Utiliser le calcul littéral dont puissances, racines carrées, identités remarquables, équation, inéquation
• Géométrie
Manipuler les vecteurs du plan dont égalité, somme, coordonnées, colinéarité, déterminant, base orthonormée
Résoudre des problèmes de géométrie dont figures planes, calcul de longueurs, angles, aires, volumes, optimisation
Représenter et caractériser les droites du plan dont vecteur directeur, équations de droite, pente, alignement, position relative de deux droites (uniquement dans le plan muni d’un repère orthonormé)
• Fonctions
Se constituer un répertoire de fonctions de référence dont fonctions carré, inverse, racine carrée, cube / courbes représentatives, résolutions graphiques ou algébriques d’équation
Représenter algébriquement et graphiquement les fonctions dont intervalle de définition, courbe représentation, parité d’une fonction, modélisation, résolution d’équations
Étudier les variations et les extremums d’une fonction dont tableau de variations, taux d’accroissement, variations des fonctions de référence
• Statistiques et probabilités
Utiliser l’information chiffrée et statistique descriptive dont proportion, pourcentage, évolution, moyenne, écart interquartile, écart type
Modéliser le hasard, calculer des probabilités dont loi de probabilité, réunion, intersection, complémentaire
Échantillonnage dont loi des grands nombres (simplifiée), estimation d’une probabilité par une fréquence observée
• Algorithmique et programmation
Utiliser les variables et les instructions élémentaires dont instruction conditionnelle, boucle bornée, bouche non bornée
Notion de fonction dont fonctions à un ou plusieurs arguments, fonction renvoyant à un nombre aléatoire
• Vocabulaire ensembliste et logique
dont symboles et notations, négation d’une proposition, contre-exemple, implication, équivalence, réciproque, raisonnements par disjonction des cas et par l’absurde
LE PROGRAMME de 1re
VISION SYNOPTIQUE DU PROGRAMME
• Algèbre
Suites numériques, modèles discrets dont suites arithmétiques, suite géométriques, sens de variation d’une suite
Équations, fonctions polynômes du second degré dont forme canonique, racines, signe, discriminant
• Analyse
Dérivation dont taux de variation, nombre dérivé, tangente à une courbe représentative, fonction dérivée (notamment des fonctions usuelles), opérations, fonction valeur absolue
Variations et courbes représentatives des fonctions dont lien entre sens de variation et signe de la fonction dérivée, nombre dérivé en un extremum
Fonction exponentielle
Fonctions trigonométriques dont cercle trigonométrique, longueur d’arc, radian, fonctions cosinus et sinus, parité, périodicité
• Géométrie
Calcul vectoriel et produit scalaire dont bilinéarité, symétrie, formule d’Al-Kashi
Géométrie repérée dont vecteur normal à une droite, équation de cercle, parabole
• Probabilités et statistiques
Probabilités conditionnelles et indépendance dont arbres pondérés, partition de l’univers, succession de deux épreuves indépendantes
Variables aléatoires réelles dont modélisation d’une expérience aléatoire, loi d’une variable aléatoire, espérance, variance, écart type
• Algorithmique et programmation
Notion de liste dont génération, manipulation, parcours
• Vocabulaire ensembliste et logique dont appartenance, inclusion, réunion, intersection, complémentaire d’un sous-ensemble, contre-exemple, implication, équivalence, réciproque, condition nécessaire / condition suffisante, statut des égalités et des lettres, quantificateurs, négation d’une proposition
LE PROGRAMME de TLE
VISION SYNOPTIQUE DU PROGRAMME
• Algèbre et géométrie
Combinatoire et dénombrement dont notions ensemblistes (produit cartésien, couple, liste, k-uplet), dénombrement (combinaisons, permutations, coefficients binomiaux).
Manipulation des vecteurs, des droites et des plans de l'espace dont calculs vectoriels et translations, combinaisons linéaires de vecteurs, indépendance linéaire, direction de droites et de plans.
Orthogonalité et distance dans l'espace dont produits scalaires, distances, orthogonalité des deux droites, d'un plan et d'une droite, projection orthogonale sur un plan, sur une droite.
Représentations paramétriques et équations cartésiennes dont représentation paramétrique d'une droite, équation cartésienne d'un plan.
• Analyse
Suites dont raisonnement par récurrence, limites d'une suite, théorème des gendarmes, opérations sur les limites, suites géométriques (qn).
Limites des fonctions dont limite finie ou infinie d'une fonction, asymptotes, limites des fonctions de référence, limites et comparaisons, opérations sur les limites.
Compléments sur la dérivation dont composée de deux fonctions, dérivée d'une fonction composée, dérivée seconde d'une fonction, convexité, point d'inflexion.
Continuité d'une fonction de variable réelle dont continuité d'une fonction en un point, sur un intervalle, image d'une suite convergente par une fonction continue, théorème des valeurs intermédiaires.
Fonction logarithme dont fonction réciproque de la fonction exponentielle, propriétés algébriques, dérivée, variations, limites, courbe représentative, croissance comparée avec la puissance en 0 et ∞
Fonction sinus et cosinus dont dérivées, variations, courbes représentatives.
Primitives, équations différentielles dont équations différentielles y' = f, notion de primitive d'une fonction continue sur un intervalle, primitives des fonctions de référence, équations différentielles de la forme y' = ay, y'= a + b
Calcul intégral dont vision graphique de l'intégrale (aire sous la couche pour une fonction continue positive sur un intervalle), calcul approché en liaison avec la méthode des rectangles, calcul exact par les primitives, linéarité, positivité et intégration des inégalités, relation de Chasles, valeur moyenne d'une fonction, intégration par parties.
• Probabilités
Succession d'épreuves indépendantes, schéma de Bernoulli dont modèles de la succession d'épreuves indépendantes ; représentation par un produit cartésien, par un arbre ; épreuve, loi et schéma de Bernoulli ; loi binomiale.
Sommes de variables aléatoires dont somme de deux variables aléatoires, linéarité de l'espérance, additivité de la variance pour des variables indépendantes ; application à l'espérance, à la variance et à l'écart type de la loi binomiale ; échantillon de taille n d'une d'une loi de probabilité, espérance variance et écart type de la somme et de la moyenne.
Concentration, loi de grands nombres dont inégalité de Biénaymé-Tchebychev, inégalité de concentration, loi des grands nombres.
• Algorithmique et programmation
dont notion de variable, type d'une variable, affectation, instruction conditionnelle, boucles, liste (générer une liste, manipuler les éléments d'une liste et leurs indices, parcourir une liste, itérer sur les éléments d'une liste)
• Vocabulaire ensembliste et logique
dont élément d'un ensemble, sous-ensemble, appartenance, inclusion, réunion ; intersection, complémentaire, et symboles correspondants ∈, ⋂, ⋃ ; notation des ensembles de nombres et des intervalles ; notion de couple, de triplet, de n-uplet ; produit cartésien ; notion de bijection ; connecteurs "et" et "ou", quantificateurs ; propositions, négation d'une d'une proposition, implication, réciproque d'une implication, contraposée ; raisonnement par disjonction des cas, par l'absurde, par contraposée, par équivalence, par récurrence ; condition nécessaire, condition suffisante.
PHYSique-chimie 2de • 1re • TLE
• La Physique-Chimie fait partie du tronc commun de la classe de 2de, à raison de 3 h par semaine.
• Dans la voie générale, à partir de la Première, la Physique-Chimie ne fait pas partie du tronc commun, et devient un enseignement de spécialité à raison de 4 h par semaine en Première et 6 h par semaine en Terminale.
LE PROGRAMME DE LA SECONDE À LA TERMINALE
PRINCIPES GÉNÉRAUX
OBJECTIFS
Le préambule du programme donne les objectifs de l’enseignement de Physique-Chimie, notamment :
• L’importance de la mise en activité des élèves
• L’importance de l’activité de modélisation, qui permet d’établir un lien entre le « monde » des objets, des expériences, des faits et le « monde » des modèles et des théories
• L’expression des conceptions initiales des élèves
• L’importance de l’approche expérimentale
• L’importance de la contextualisation qui permet de donner du sens aux apprentissages
• La nécessité de procéder à des synthèses
• L’intérêt de faire des liens entre les notions du programme et avec les autres disciplines
• L’intérêt de mettre en perspective les savoir grâce à l’histoire des sciences et l’actualité scientifique
• L’intérêt de communiquer à l’écrit comme à l’oral, notamment pour présenter une démarche, échanger entre pairs, argumenter, préciser sa pensée (et développer ainsi ses capacités langagières à l’oral, en vu de l’épreuve oral du Baccalauréat)
• Le recours à des résolutions de problèmes (qui est encouragé pour l’acquisition des compétences de la démarche scientifique)
PRÉSENTATION DU PROGRAMME
• Contrairement au programme de 2010 organisé selon trois thèmes de contextualisation (santé, sport, Univers), les nouveaux programmes sont organisés selon des parties notionnelles, dans la continuité du Cycle 4.
• Le travail sur la mesure et les incertitudes commence dès la classe de Seconde.
• Au début de chaque partie ou sous-partie figure une indication des notions étudiées au cycle 4 ou en Seconde
• La colonne de droite des tableaux s’appelle désormais « Capacités exigibles » (au lieu de compétences attendues)
• Parmi ces capacités figurent :
- des capacités mathématiques (> liste de ces capacités dans le PDF à télécharger)
- des capacités numériques, autour de la programmation (le langage choisi est Python) et des microcontrôleurs, de type Arduino (> liste de ces capacités dans le PDF à télécharger)
• En 1re, une liste des capacités expérimentales à faire acquérir aux élèves dans le cadre des activités expérimentales est établie (> liste dans le PDF à télécharger)
LE PROGRAMME de 2de
VISION SYNOPTIQUE DU PROGRAMME
• Mesure et incertitudes
Variabilité de la mesure d’une grandeur physique, Incertitude-type, Ecriture du résultat, Valeur de référence
• Constitution et transformations de la matière
Constitution de la matière de l’échelle macroscopique à l’échelle microscopique
Description et caractérisation de la matière à l’échelle macroscopique dont corps purs et mélanges (espèce chimique, identification, composition massique et volumique), solutions aqueuses (solvant, soluté, concentration massique, dosage par étalonnage)
Modélisation de la matière à l’échelle microscopique dont passage du macroscopique au microscopique (espèces moléculaires, ioniques, électroneutralité au niveau macro, molécules, atomes, ions), noyau de l’atome (numéro atomique, nombre de masse, masse et charge des constituants du noyau, neutralité de l’atome), cortège électronique (configuration électronique, électrons de valence, familles chimiques), stabilité chimique (gaz nobles, ions monoatomiques, molécules, modèle de Lewis, énergie de liaison), la mole
Modélisation des transformations de la matière et transferts d’énergie
Transformation physique dont écriture symbolique d’un changement d’état, modélisation microscopique, transformations endothermiques et exothermiques, énergie de changement d’état
Transformation chimique dont réaction chimique, équation de réaction, espèce spectatrice, stœchiométrie, réactif limitant, transformations endothermiques et exothermiques, synthèse d’une espèce chimique présente dans la nature
Transformation nucléaire dont isotopes, écriture symbolique d’une réaction nucléaire, aspects énergétiques
• Mouvement et interactions
Décrire un mouvement dont système, référentiel, relativité du mouvement, modélisation par un point, position, trajectoire, vecteur déplacement ; vecteur vitesse moyenne, vecteur vitesse, mouvement rectiligne
Modéliser une action sur un système dont modélisation d’une action par une force, principe des actions réciproques, caractéristiques d’une force
Principe d’inertie dont modèle du point matériel, principe d’inertie, cas d’immobilité ou de mouvement rectiligne uniforme, chute libre à une dimension
• Ondes et signaux
Émission et perception d’un son dont vitesse de propagation d’un signal sonore, périodicité, fréquence et période, hauteur, timbre, amplitude, intensité sonore, niveau d’intensité sonore
Vision et images dont propagation rectiligne de la lumière, vitesse de propagation, lumière blanc, lumière colorée, spectres d’émissions, longueur d’onde, lois de Snell-Descartes, dispersion, lentilles (lentille mince convergente, foyers, distance focale, image réelle d’un objet réelle, grandissement, modèle de l’œil réduit)
Signaux et capteurs dont loi des nœuds, loi des mailles, caractéristique d’un dipôle, dipôle ohmique, lois d’Ohm, capteurs électriques
LE PROGRAMME de 1re
VISION SYNOPTIQUE DU PROGRAMME
• Mesure et incertitudes
Variabilité de la mesure d’une grandeur physique
Incertitude-type dont évaluations de type A et de type B
Écriture du résultat
Valeur de référence
• Constitution et transformations de la matière
Suivi de l’évolution d’un système, siège d’une transformation
Détermination de la composition du système initial à l’aide de grandeurs physiques dont masse molaire, volume molaire, concentration en quantité de matière, absorbance, loi de Beer-Lambert
Suivi et modélisation de l’évolution d’un système chimique dont réaction d’oxydo-réduction, tableau d’avancement, stœchiométrie
Détermination d’une quantité de matière grâce à une transformation chimique dont titrage avec repérage colorimétrique de l’équivalence, équivalence
De la structure des entités aux propriétés physiques de la matière
De la structure à la polarité d’une entité dont schéma de Lewis, géométrie des entités, électronégativité, polarisation d’une liaison covalente, polarité d’une entité moléculaire
De la structure des entités à la cohésion et à la solubilité/miscibilité d’espèces chimiques dont cohésion dans un solide, pont hydrogène, dissolution des solides ioniques dans l’eau, extraction par solvant, solubilité, miscibilité, hydrophilie, lipophilie, amphiphilie
Propriétés physico-chimiques, synthèses et combustions d’espèces chimiques organiques
Structure des entités organiques dont formules brutes et semi-développées, groupes caractéristiques et familles fonctionnelles, spectroscopie infrarouge
Synthèses d’espèces chimiques organiques dont étapes d’un protocole de synthèse, rendement d’une synthèse
Conversion de l’énergie stockée dans la matière organique dont combustion, énergie molaire de réaction, pouvoir calorifique massique, enjeux de société
• Mouvement et interactions
Interactions fondamentales et introduction à la notion de champ dont charge électrique, interaction électrostatique, loi de Coulomb, force et champ de gravitation, force et champ électrostatique
Description d’un fluide au repos dont masse volumique, pression, température, loi de Mariotte, forces pressantes, loi fondamentale de la statique des fluides
Mouvement d’un système dont vecteur variation de vitesse, lien entre variation du vecteur vitesse et somme des forces, rôle de la masse
• L’énergie : conversions et transferts
Aspects énergétiques des phénomènes électriques dont porteur de charge, lien intensité et débit de charges, modèle source réelle de tensions continue, puissance et énergie, effet Joule, rendement d’un convertisseur
Aspects énergétiques des phénomènes mécaniques dont énergie cinétique, travail d’une force, théorème de l’énergie cinétique, énergie potentielle de pesanteur, forces conservatives et non conservatives, énergie mécanique, conservation et non-conservation de l’énergie mécanique, gain ou dissipation d’énergie
• Ondes et signaux
Ondes mécaniques dont onde mécanique progressive, célérité d’une onde, ondes mécaniques périodiques, ondes sinusoïdales, relation entre période, longueur d’onde et célérité
La lumière : images et couleurs, modèles ondulatoire et particulaire
Images et couleurs dont relation de conjugaison d’une lentille mince convergente, grandissement, image réelle, image virtuelle, image droite, image renversée, couleur des objets, synthèses additive et soustractive, absorption, diffusion, transmission, vision des couleurs et trichromie
Modèles ondulatoire et particulaire de la lumière dont domaines des ondes électromagnétiques, relation entre longueur d’onde, célérité de la lumière et fréquence, photo, interaction lumière-matière (absorption, émission), quantification des niveaux d’énergie
LE PROGRAMME de TLE
VISION SYNOPTIQUE DU PROGRAMME
• Mesure et incertitudes
Variabilité de la mesure d’une grandeur physique
Incertitude-type dont évaluations de type A et de type B
Écriture du résultat
Valeur de référence
• Constitution et transformations de la matière
Déterminer la composition d'un système par des méthodes physiques et chimiques
Modéliser des transformations acide-base par des transferts d'ion hydrogène H+ dont acide et base de Brönsted, couple et réaction acide-base, espèce amphotère, couples acide-base de l'eau, de l'acide carbonique, d'acides carboxyliques, d'amines.
Analyser un système chimique par des méthodes physiques dont relations pH et [H3O+], absorbance, loi de Beer-Lambert, conductance, conductivité, loi de Kaulrausch, courbe d'étalonnage, spectroscopie infrarouge et UV-visible
Analyser un système par des méthodes chimiques dont titre massique et densité d’une solution, titrage avec suivi pH-métrique et titrage avec suivi conductimétrique
Modéliser l'évolution temporelle d'un système, siège d'une transformation
Suivre et modéliser l'évolution temporelle d'un système siège d'une transformation chimique
Suivi temporel et modélisation macroscopique dont transformations lentes et rapides, factures cinétiques, catalyse, vitesse volumique de disparition d’un réactif et d’apparition d’un produit, loi de vitesse d’ordre 1
Modélisation microscopique dont mécanisme réactionnel, modification par ajout d’un catalyseur, influence des facteurs cinétiques
Modéliser l'évolution temporelle d'un système, siège d'une transformation nucléaire dont décroissance radioactive, diagramme (N,Z), radioactivité α, β et γ, équation d’une réaction nucléaire et lois de conservation, constante radioactive, loi de décroissance, temps de demi-vie, activité, applications (datation, domaine médical, protection)
Prévoir l'état final d'un système, siège d'une transformation chimique
Prévoir le sens de l'évolution spontanée d'un système chimique dont transformation non totale, équilibre chimique, modèle de l’équilibre dynamique, quotient de réaction, constante d’équilibre, critère d’évolution d’un système hors équilibre chimique, réaction d’oxydo-réduction, pile, demi-piles, pont salin ou membrane, tension à vide, fonctionnement, usure et capacité électrique d’une pile, oxydants et réducteurs usuels
Comparer la force des acides et des bases dont constante d’acidité, produit ionique de l’eau, réaction d’un acide ou d’une base avec l’eau, cas limite des acides forts et des bases fortes dans l’eau, solutions courantes d’acides et de bases, diagrammes de prédominance et de distribution, solution tampon
Forcer le sens d'évolution d'un système dont passage forcé d’un courant pour réaliser une transformation chimique, électrolyseur, stockage et conversion d’énergie chimique
Élaborer des stratégies en synthèse organique
Structures et propriétés dont formule topologique, esters, amines, aides et halogénoalcanes, squelettes carbonés instaurés, cycliques, isomérie de constitution, polymères
Optimisation d'une étape de synthèse dont optimisation de la vitesse de formation d’un produit et du rendement d’une synthèse
Stratégie de synthèse multi-étapes dont modification de groupe caractéristique et de chaîne carbonée, polymérisation, protection/déprotection, synthèses éco-responsables
• Mouvement et interactions
Décrire un mouvement dont vecteurs position, vitesse, accélération d’un point, coordonnées des vecteurs vitesse et accélération dans le repère de Frenet pour un mouvement circulaire, mouvement rectiligne uniformément accéléré, mouvement circulaire uniforme
Relier les actions appliquées à un système à son mouvement
Deuxième loi de Newton dont centre de masse, référentiel galiléen, deuxième loi de Newton, équilibre d’un système
Mouvement dans un champ uniforme dont champ électrique créé par un condensateur plan, mouvement d’une particule dans un champ uniforme, accélérateur linéaire de particules chargées, aspects énergétiques
Mouvement dans un champ de gravitation dont mouvement des satellites et des planètes, orbite, lois de Kepler, période de révolution, satellite géostationnaire
Modéliser l'écoulement d'un fluide
dont poussée d’Archimède, écoulement d’un fluide en régime permanent, débit volumique d’un fluide incompressible, relation de Bernoulli, effet Venturi
• L'énergie : conversions et transferts
Décrire un système thermodynamique : exemple du modèle du gaz parfait
dont masse volumique, température thermodynamique, pression, équation d’état du gaz parfait
Effectuer des bilans d'énergie sur un système : le premier principe de la thermodynamique
dont énergie interne, aspects microscopiques, transfert thermique, travail, capacité thermique et énergie interne d’un système incompressible, modes de transfert thermique, flux thermique, résistance thermique, bilan thermique du système Terre-atmosphère, effet de serre, loi phénoménologique de Newton
• Ondes et signaux
Caractériser les phénomènes ondulatoires
dont intensité sonore, niveau d’intensité sonore, atténuation, diffraction d’une onde par une ouverture, angle caractéristique de diffraction, interférence de deux ondes, conditions d’observation, interférence constructives et destructives, interférences de deux ondes lumineuses, différence de chemin optique, effet Doppler, décalage Doppler
Former des images, décrire la lumière d'un flux de photons
Former des images dont modèle de la lunette astronomique, grossissement
Décrire la lumière par un flux de photons dont photon, effet photoélectrique, travail d’extraction, absorption et émission de photons, enjeux énergétiques (rendement d’une cellule photovoltaïque)
Étudier la dynamique d'un système électrique
dont intensité d’un courant électrique en régime variable, comportement capacitif, modèle du condensateur, relation entre charge et tension, capacité d’un condensateur, modèle du circuit RC série (charge, décharge, temps caractéristique), capteurs capacitifs
> Voir le B.O. de Physique-Chimie 2de
> Voir le B.O. de Physique-Chimie 1re
> Voir le B.O. de Physique-Chimie Tle
SVT 2de • 1re
Les SVT font partie du tronc commun de la classe de 2de, à raison de 1 h 30 par semaine.
Dans la voie générale, à partir de la Première, les SVT ne font pas partie du tronc commun, et deviennent un enseignement de spécialité à raison de 4 h par semaine en Première (et 6 h par semaine en Terminale).
LE PROGRAMME DE SECONDE, CONTINUITÉ ENTRE CYCLE 4 ET PREMIÈRE

PRINCIPES GÉNÉRAUX
OBJECTIFS
Le préambule du programme donne les objectifs de l’enseignement des SVT en classe de 2deet 1re, notamment :
• l’importance de la formation civique des élèves, en développant leur esprit critique et en les éduquant aux médias et à l’information (vérification de source, légitimité, fiabilité des informations), afin de les armer face aux publications « pseudo-scientifiques », voire idéologiques
• l’importance d’aider les élèves dans leur orientation, en leur faisant découvrir des métiers liés aux sciences et en leur faisant découvrir les études scientifiques possibles dans l’enseignement supérieur et les métiers auxquels elles conduisent
• la place centrale des activités expérimentales et l’importance des démarches et stratégies associées
• l’importance de la pratique de l’oral, notamment argumenter, préciser sa pensée, expliciter son raisonnement
• l’intérêt des outils numériques (Internet, tableur, ExAO, capteurs connectés à des microcontrôleurs programmables (de type Arduino), bases de données, systèmes d’informations géoscientifiques, modélisation numérique, programmation, réalité virtuelle et réalité augmentée)
• l’importance du lien avec les autres disciplines
LA PRÉSENTATION DU PROGRAMME
• Les contenus ne sont plus organisés en tableaux, mais selon les paragraphes suivants :
- Connaissances : Notions fondamentales - Objectifs
- Capacités : Précisions
LE PROGRAMME de 2de
• La Terre, la vie et l’organisation du vivant
L’organisation fonctionnelle du vivant
L’organisme pluricellulaire, un ensemble de cellules spécialisées : Notions fondamentales : cellule, matrice extracellulaire/paroi, tissu, organe ; organite, spécialisation cellulaire, ADN, double hélice, nucléotides (adénine, thymine, cytosine, guanine), complémentarité, gène, séquence
Le métabolisme des cellules : Notions fondamentales : métabolisme, autotrophe, hétérotrophe, organites, enzymes
Biodiversité, résultat et étape de l’évolution
Les échelles de la biodiversité : Notions fondamentales : biodiversité, échelles de biodiversité, variabilité, mutation, allèle
La biodiversité change au cours du temps : Notions fondamentales : espèces, variabilité, crise biologique, extinction massive et diversification
L’évolution de la biodiversité au cours du temps s’explique par des forces évolutives s’exerçant au niveau des populations : Notions fondamentales : maintien des formes aptes à se reproduire, hasard/aléatoire, sélection naturelle, effectifs, fréquence allélique, variation, population, ressources limitées
Communication intra-spécifique et sélection sexuelle : Notions fondamentales : communication, émetteur, récepteur, comportement, vie solitaire, vie en société, dimorphisme sexuel
• Les enjeux contemporains de la planète
Géosciences et dynamique des paysages
L’érosion, processus et conséquences : Notions fondamentales : érosion, altération, modes de transports, sédiments
Sédimentation et milieux de sédimentation : Notions fondamentales : sédiments, roche détritique, milieu de sédimentation
Érosion et activité humaine
Agrosystèmes et développement durable
Structure et fonctionnement des agrosystèmes : Notions fondamentales : système ; agrosystème ; intrants (dont engrais et produits phytosanitaires) ; exportation ; biomasse ; production ; rendement écologique
Caractéristiques des sols et production de biomasse : Notions fondamentales : notion de biomasse ; réseaux trophiques ; décomposeurs ; cycle de matière
Vers une gestion durable des agrosystèmes
• Corps humain et santé
Procréation et sexualité humaine
Corps humain : de la fécondation à la puberté : Notions fondamentales : hormones sexuelles (testostérone, progestérone, œstrogènes) ; organes cibles, follicules ; corps jaune ; cellules interstitielles ; tubes séminifères ; gène SrY ; gonades indifférenciées et différenciées
Cerveau, plaisir, sexualité : Notions fondamentales : composante biologique de la relation entre sexualité et plaisir ; cerveau et système de récompense/plaisir dans l’espèce humaine ; structures cérébrales et composantes affectives, motivationnelles et cognitives
Hormones et procréation humaine : Notions fondamentales : hormones et neurohormones hypothalamo-hypophysaires (FSH, LH et GnRH) ; modes d’action biologique des molécules exogènes
Micro-organismes et santé
Agents pathogènes et maladies vectorielles : Notions fondamentales : pathogène, vecteur, réservoir à pathogène, cycle évolutif, épidémie/endémie, modes de transmission, traitements, prophylaxie, vaccins, porteur sain
Microbiote humain et santé : Notions fondamentales : symbiose ; hôte et microbiote ; unicité et diversité du microbiote ; habitudes alimentaires et évolution du microbiote ; microbiote maternel et construction de la symbiose hôte-microbiote ; compétition entre microbes
Le programme de 1re
• La Terre, la vie et l’organisation du vivant
Transmission, variation et expression du patrimoine génétique
Les divisions cellulaires des eucaryotes : Notions fondamentales : diploïde, haploïde, méiose, phases du cycle cellulaire eucaryote : G1, S (synthèse d’ADN), G2, mitose (division cellulaire), fuseau mitotique ou méiotique
La réplication de l’ADN : Notions fondamentales : réplication semi conservative, ADN polymérase, clone
Mutations de l’ADN et variabilité génétique : Notions fondamentales : allèles, mutations, nature et fréquence des mutations, mutations spontanées et induites, systèmes de réparation, ADN polymérase
L’histoire humaine lue dans son génome
L’expression du patrimoine génétique : Notions fondamentales : transcription, traduction, pré-ARNm, ARNm, codon, riboses, génotype, phénotype
Les enzymes, des biomolécules aux propriétés catalytiques : Notions fondamentales : catalyse, substrat, produit, spécificité
La dynamique interne de la Terre
La structure du globe terrestre
L’apport des études sismologiques et thermiques à la connaissance du globe terrestre : Notions fondamentales : contraintes, transmission des ondes sismiques, failles, réflexion, réfraction, zones d’ombre
La dynamique de la lithosphère
La caractérisation de la mobilité horizontale
La dynamique des zones de divergence
La dynamique des zones de convergence (zones de subduction / zones de collision) : Notions fondamentales pour l’ensemble du sous-thème « La dynamique de la lithosphère » : morphologie d’une dorsale et d’une zone de subduction, failles normales et inverses, remontée asthénosphérique, magmatisme et roches associées, hydrothermalisme, augmentation de densité, panneau plongeant, fusion partielle, déformation, plis, chevauchement
• Enjeux contemporains de la planète
Écosystèmes et services environnementaux
Les écosystèmes : des interactions dynamiques entre les êtres vivants et entre eux et leur milieu
L’humanité et les écosystèmes : les services écosystémiques et leur gestion : Notions fondamentales : écosystème, interactions, biodiversité, relations interspécifiques, équilibre dynamique, services écosystémiques
• Corps humain et santé
Variation génétique et santé
Mutations et santé
Patrimoine génétique et santé
Altérations du génome et cancérisation : notions fondamentales : mutations, cancérisation, facteurs de risques
Variation génétique bactérienne et résistance aux antibiotiques
Le fonctionnement du système immunitaire humain
L’immunité innée : notions fondamentales : organes lymphoïdes, macrophages, phagocytose, médiateurs chimiques de l’inflammation, interleukines, récepteurs de surface, réaction inflammatoire, médicaments anti-inflammatoires
L’immunité adaptative : notions fondamentales : cellules présentatrices de l’antigène, lymphocytes B, plasmocytes, immunoglobulines (anticorps), lymphocytes T CD4, lymphocytes T auxiliaire, lymphocytes T CD8, lymphocytes T cytotoxiques ; sélection, amplification (expansion) et différenciation clonale
L’utilisation de l’immunité adaptative en santé humaine
enseignement scientifique 1re • TLE
L’enseignement scientifique fait partie du tronc commun, à raison de 2 h par semaine en Première et en Terminale.
PRINCIPES GÉNÉRAUX
Le préambule du programme définit les grandes lignes de l’enseignement scientifique en classe de 1re, notamment :
• La nécessité de transmettre une culture scientifique
• La pratique de la démarche scientifique, notamment via l’observation et l’expérience
• L’importance de l’étude de l’histoire raisonnée des sciences
• L’importance des mathématiques
Et en classe de Tle :
• Mieux comprendre le monde, son organisation, son fonctionnement et les lois qui le régissent
• Comprendre comment le savoir scientifique se construit
• Pratiquer la démarche scientifique
• Prendre conscience de l'impact des activités humaines sur son environnement immédiat et à l'échelle de la planète
• Participer à la prise de décisions par une approche scientifique
OBJECTIFS GÉNÉRAUX DE FORMATION
Le programme définit trois objectifs généraux de formation qui doivent être mobilisés tout au long de l’apprentissage des notions thématiques :
• Comprendre la nature du savoir scientifique et ses méthodes d’élaboration
• Identifier et mettre en œuvre des pratiques scientifiques
• Identifier et comprendre les effets de la science sur les sociétés et sur l’environnement
PRÉSENTATION DU PROGRAMME
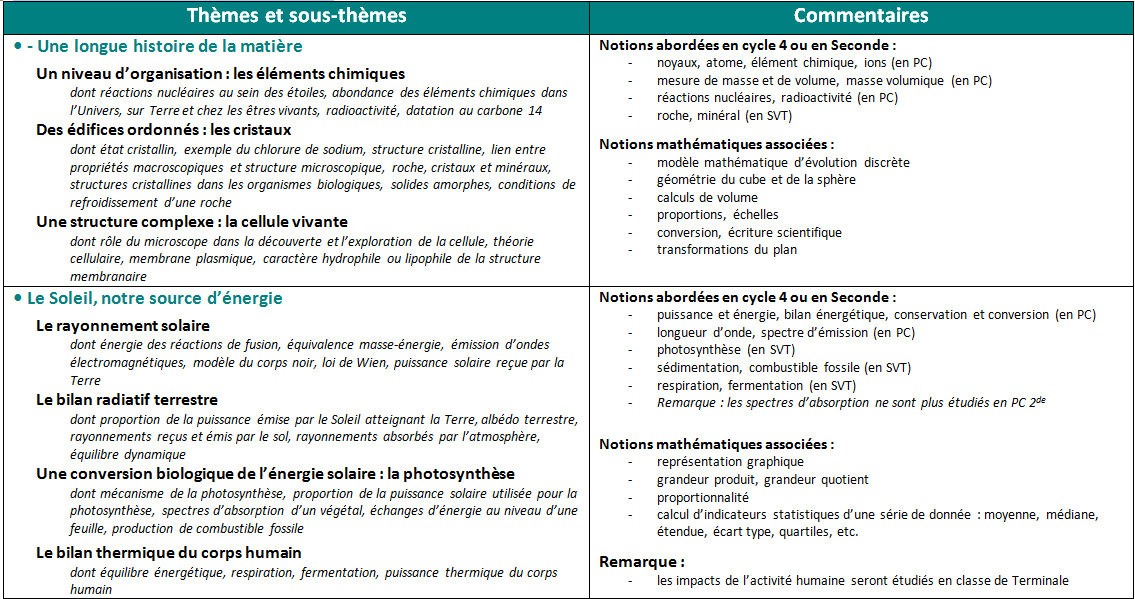
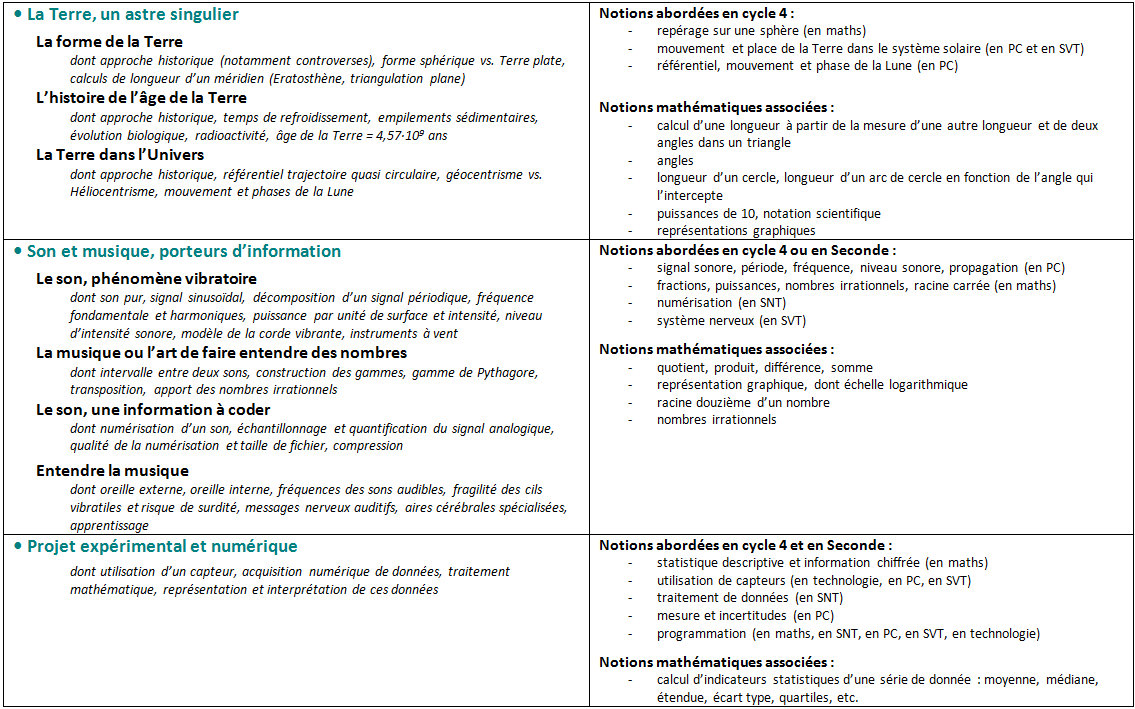
• Le programme est structuré autour de 4 thèmes en 1re (Une longue histoire de la matière ; Le Soleil, notre source d’énergie ; La Terre, un astre singulier ; Son et musique, porteurs d’information) + d’un projet expérimental et numérique (à effectuer sur 12 h, soit l’équivalent de 6 semaines) ; et de 3 thèmes en Tle (Science, climat et société ; Le futur des énergies ; Une histoire du vivant)
• Au début de chaque thème figure une rubrique « histoire, enjeux et débats » donnant des exemples d’éléments historiques et de questions socialement vives en lien avec le thème. Dans chaque thème, au moins un des items de cette liste doit être abordé.
• Chaque sous-thème est ainsi présenté :
- Une courte introduction pour décrire l’objectif du sous thème
- Un tableau présentant les savoirs en vis à-vis des savoir-faire exigibles
- Les prérequis et limites du sous-thème
PROGRAMME DE 1RE
VISION SYNOPTIQUE DU PROGRAMME
PROGRAMME DE TLE
VISION SYNOPTIQUE DU PROGRAMME
• Science, climat et société
L'atmosphère terrestre et la vie
Évolution de la composition de l’atmosphère au cours des temps géologiques, formation de l’hydrosphère et premières traces de vie ; sources et puits de dioxygène (O2) actuels ; effets du rayonnement solaire et couche d’ozone ; cycle du carbone, carbone d’origine anthropique
La complexité du système climatique
Grandeurs atmosphériques, climatologie/météorologie, indicateurs du climat ; variabilité naturelle ; émission de GES et réchauffement climatique ; dynamique du système climatique : équilibre radiatif, perturbations, rétroactions positives, rôle des océans ; rétroactions négatives
Le climat du futur
Paramètres de l’évolution climatique et modèles climatiques ; évaluation des résultats des modèles et conclusions scientifiques ; probabilités, lien de cause à effet/corrélation ; projections climatiques consensuelles en lien avec les émissions de GES
Énergie, choix de développement et futur climatique
Les différentes sources d’énergie, données de production et d’utilisation dans le monde ; énergie et puissance ; qualité de l’air ; notion d’empreinte carbone ; scénarios de transition écologique ; impacts sur la santé
• Le futur des énergies
Deux siècles d'énergie électrique
Évolution des idées en physique (induction avec Faraday, Maxwell, mécanique quantique et comportement probabiliste), rendement d’un alternateur, spectres d’absorption, semi-conducteurs, capteurs photovoltaïques
Les atouts de l'électricité
Modes d’obtention d’énergie électrique sans combustion (par conversion d’énergie mécanique, conversion d’énergie radiative reçue du Soleil ou conversion électrochimique), impacts sur l’environnement et risques, intermittence, stockage
Optimisation du transport de l'électricité
Description d’un réseau de transport et de distribution électrique, minimisation des pertes par effet Joule, modélisation expérimentale d’une ligne haute tension, modélisation et optimisation d’un réseau par un graphe orienté
Choix énergétiques et impacts sur les sociétés
Impacts des choix énergétiques, critères de choix (disponibilité, impact, risques, conséquences économiques et sociales, etc.), transition énergétique et écologique, responsabilités individuelles et collectives
• Une histoire du vivant
La biodiversité et son évolution
Mesure de la biodiversité, estimations de l’effectif d’une population, d’un paramètre ; évolution biologique des fréquences alléliques : écart des résultats du modèle de Hardy-Weinberg et des fréquences alléliques naturelles
L'évolution comme grille de lecture du monde
Mobilisation de concepts évolutionniste pour expliquer une structure anatomique complexe (oeil), une particularité (difficultés obstétriques, téton masculin, etc.) ; évolution rapide des organismes microbiens, prophylaxie, résistance des ravageurs des cultures
L'évolution humaine
Similitudes génétiques et morpho-anatomiques avec le groupe des Primates ; innovations évolutives communes, arbre phylogénétique ; analyse comparée de fossiles du genre Homo ; transmission non génétique
Les modèles démographiques
Grandeur discrète, suite arithmétique, modèle linéaire, variation exponentielle d’une grandeur discrète, suite géométrique, modèle démographique de Malthus
L'intelligence artificielle
Histoire de l’ordinateur, traitement de données, langage de programmation (Python, Scratch), bugs, intelligence artificielle, apprentissage machine, inférence bayésienne
> Voir le B.O. Enseignement Scientifique 1re
> Voir le B.O. Enseignement Scientifique Tle

